104深度分页

前言

最近遇到接口慢查询问题，仔细排查发现涉及mysql深度分页问题，于是便查阅各种资料寻求解决方案。这里总结一下可能会用到的解决方案。

我们日常做分页需求时，一般会用limit实现，但是当偏移量特别大的时候，查询效率就变得低下。本文将分4个方案，讨论如何优化MySQL大量数据的深分页问题。

limit深度分页为什么会变慢？

先看下表结构：

CREATE TABLE account (
  id int(11) NOT NULL AUTO_INCREMENT COMMENT '主键Id',
  name varchar(255) DEFAULT NULL COMMENT '账户名',
  balance int(11) DEFAULT NULL COMMENT '余额',
  create_time datetime NOT NULL COMMENT '创建时间',
  update_time datetime NOT NULL ON UPDATE CURRENT_TIMESTAMP COMMENT '更新时间',
  PRIMARY KEY (id),
  KEY idx_name (name),
  KEY idx_update_time (update_time) //索引
) ENGINE=InnoDB AUTO_INCREMENT=1570068 DEFAULT CHARSET=utf8 ROW_FORMAT=REDUNDANT COMMENT='账户表';

假设深分页的执行SQL如下：

select id,name,balance from account where update_time> '2020-09-19' limit 100000,10;

这个SQL的执行时间如下：

执行完需要0.742秒，深分页为什么会变慢呢？如果换成 limit 0,10，只需要0.006秒哦

我们先来看下这个SQL的执行流程：

1. 通过普通二级索引树idx_update_time，过滤update_time条件，找到满足条件的记录ID。
2. 通过ID，回到主键索引树，找到满足记录的行，然后取出展示的列（回表）
3. 扫描满足条件的100010行，然后扔掉前100000行，返回。

SQL的执行流程

执行计划如下：

SQL变慢原因有两个：

1. limit语句会先扫描offset+n行，然后再丢弃掉前offset行，返回后n行数据。也就是说limit 100000,10，就会扫描100010行，而limit 0,10，只扫描10行。
2. limit 100000,10 扫描更多的行数，也意味着回表更多的次数。

通过子查询优化

因为以上的SQL，回表了100010次，实际上，我们只需要10条数据，也就是我们只需要10次回表其实就够了。因此，我们可以通过减少回表次数来优化。

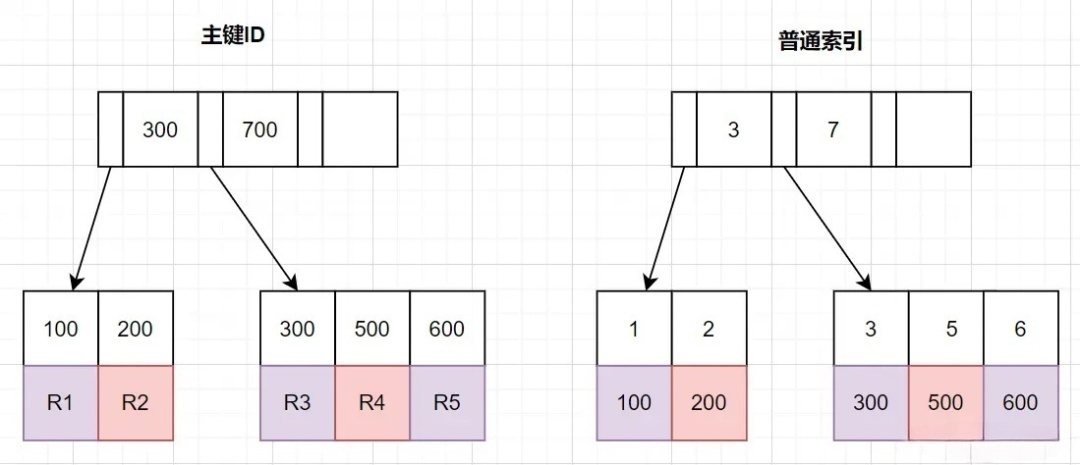
回顾B+ 树结构

那么，如何减少回表次数呢？我们先来复习下B+树索引结构哈~

InnoDB中，索引分主键索引（聚簇索引）和二级索引

• 主键索引，叶子节点存放的是整行数据
• 二级索引，叶子节点存放的是主键的值。

把条件转移到主键索引树

如果我们把查询条件，转移回到主键索引树，那就不就可以减少回表次数啦。转移到主键索引树查询的话，查询条件得改为主键id了，之前SQL的update_time这些条件咋办呢？抽到子查询那里嘛~

子查询那里怎么抽的呢？因为二级索引叶子节点是有主键ID的，所以我们直接根据update_time来查主键ID即可，同时我们把 limit 100000的条件，也转移到子查询，完整SQL如下：

select id,name,balance FROM account where id >= (select a.id from account a where a.update_time >= '2020-09-19' limit 100000, 1) LIMIT 10;（可以加下时间条件到外面的主查询）

查询效果一样的，执行时间只需要0.038秒！

我们来看下执行计划

由执行计划得知，子查询 table a查询是用到了idx_update_time索引。首先在索引上拿到了聚集索引的主键ID,省去了回表操作，然后第二查询直接根据第一个查询的 ID往后再去查10个就可以了!

因此，这个方案是可以的~

INNER JOIN 延迟关联

延迟关联的优化思路，跟子查询的优化思路其实是一样的：都是把条件转移到主键索引树，然后减少回表。不同点是，延迟关联使用了inner join代替子查询。

优化后的SQL如下：

SELECT  acct1.id,acct1.name,acct1.balance FROM account acct1 INNER JOIN (SELECT a.id FROM account a WHERE a.update_time >= '2020-09-19' ORDER BY a.update_time LIMIT 100000, 10) AS  acct2 on acct1.id= acct2.id;

查询效果也是杠杆的，只需要0.034秒

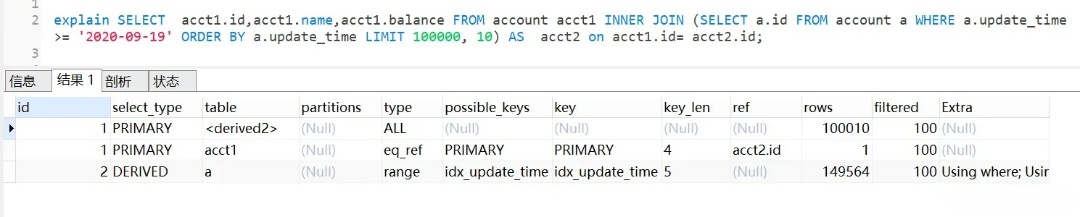
执行计划如下：

查询思路就是，先通过idx_update_time二级索引树查询到满足条件的主键ID，再与原表通过主键ID内连接，这样后面直接走了主键索引了，同时也减少了回表。

标签记录法(游标)

limit 深分页问题的本质原因就是：偏移量（offset）越大，mysql就会扫描越多的行，然后再抛弃掉。这样就导致查询性能的下降。

其实我们可以采用标签记录法，就是标记一下上次查询到哪一条了，下次再来查的时候，从该条开始往下扫描。就好像看书一样，上次看到哪里了，你就折叠一下或者夹个书签，下次来看的时候，直接就翻到啦。

假设上一次记录到100000，则SQL可以修改为：

select  id,name,balance FROM account where id > 100000 order by id limit 10;

这样的话，后面无论翻多少页，性能都会不错的，因为命中了id索引。但是你，这种方式有局限性：需要一种类似连续自增的字段。

使用between…and…

很多时候，可以将limit查询转换为已知位置的查询，这样MySQL通过范围扫描between...and，就能获得到对应的结果。

如果知道边界值为100000，100010后，就可以这样优化：

select  id,name,balance FROM account where id between 100000 and 100010 order by id desc;

3层b+树

接下来，通过以下计算步骤，就可以统计出两层的B+数大概可以存储多少条记录数据——

一、先计算一个节点的字节大小：16kb * 1024 = 16384 字节。

二、16384 字节 / 14 字节 = 1170 ，意味着，根节点有1170个页地址指针，然后，每个页地址指针指向的叶子节点可以存放16条数据。

三、那么，根据“根节点页地址指针数量 * 单个叶子节点记录行数”，计算1170 * 16 = 18720 条记录，可见，两层B+数可以存放18720条记录，当然，这个数字是存在出入的，只是作为参考。

既然已经知道两层B+数可以存放18720条数据，那么，三层不就可以进一步算出了吗？

简单画一个三层B+数的存放数据计算逻辑——

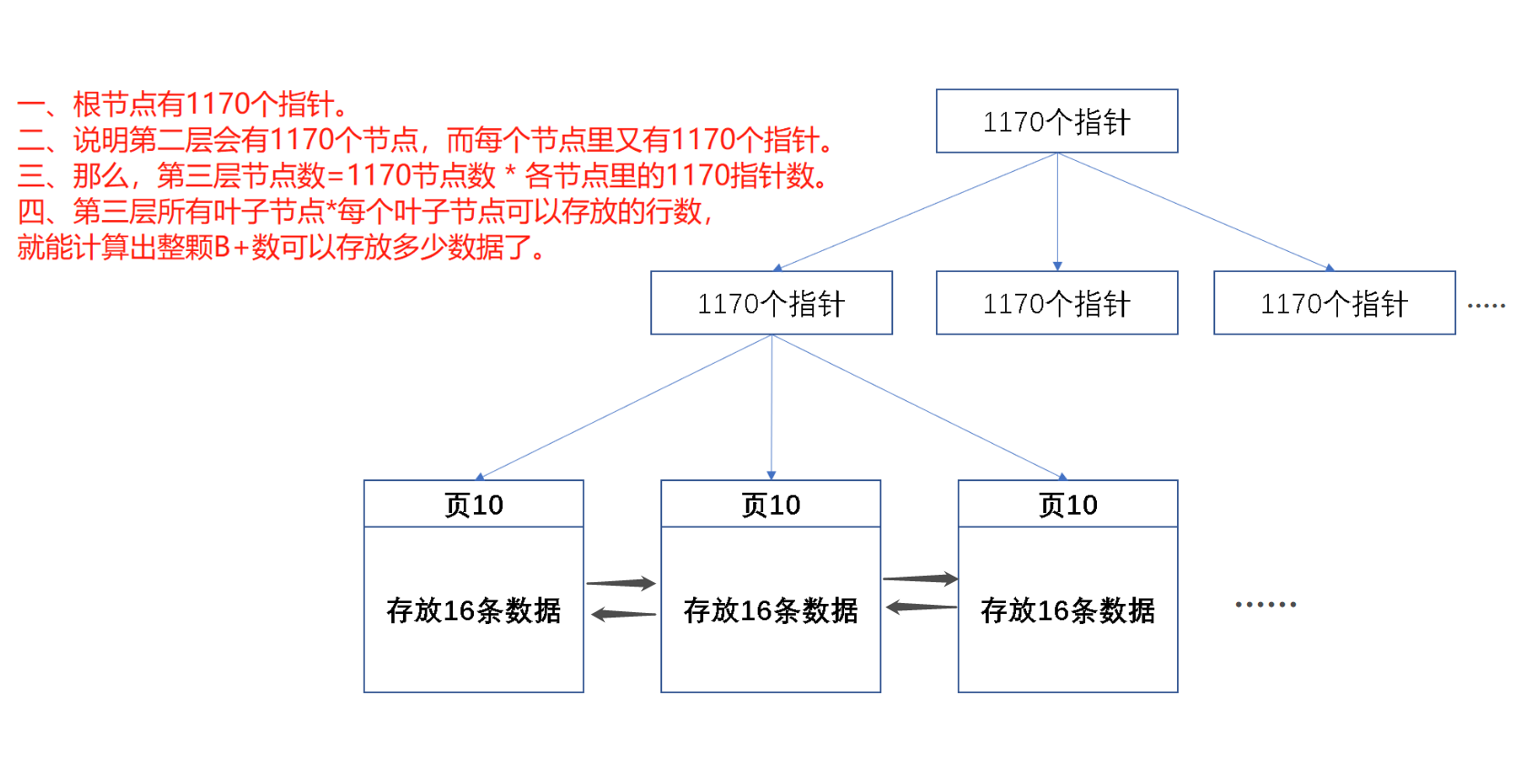
一、根节点最多有1170个指针数；

二、说明第二层最多会有1170个子节点，同时，每个子节点里最多有1170个指针数；

三、那么，第三层叶节点数量，可以通过 “第二层最多有1170个节点数量 * 每个节点里最多有1170个指针数量”，也就是1170 * 1170

四、最后，计算第三层所有叶子数量 * 各个叶子节点存放的16条数据；

最后，1170 * 1170 * 16 = 21902400，得出两千万左右条数据。

综上所述，若面试当中遇到这样问题，可以按照这个流程计算回答。