右视图

199. 二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

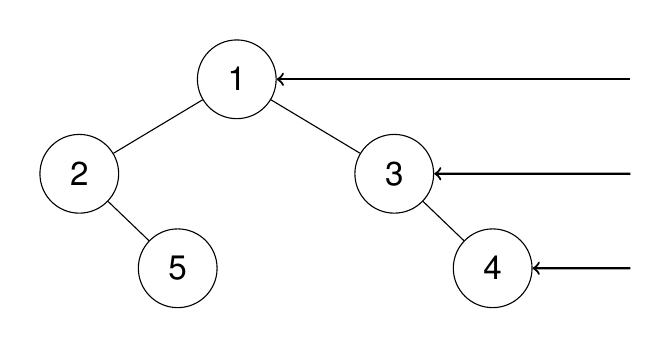
**输入：**root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

示例 2：

**输入：**root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

示例 3：

**输入：**root = [1,null,3]

输出：[1,3]

示例 4：

**输入：**root = []

输出：[]

提示:

• 二叉树的节点个数的范围是 [0,100]
• -100 <= Node.val <= 100

题解

方法一：深度优先搜索
思路

我们对树进行深度优先搜索，在搜索过程中，我们总是先访问右子树。那么对于每一层来说，我们在这层见到的第一个结点一定是最右边的结点。

算法

这样一来，我们可以存储在每个深度访问的第一个结点，一旦我们知道了树的层数，就可以得到最终的结果数组。

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> ans = new LinkedList<>();
        dfs(root, 1, ans);
        return ans;
    }
    
    public void dfs(TreeNode node, int i, List<Integer> ans) {
        if (node == null) {
            return;
        }
        if (i > ans.size()) {
            ans.add(node.val);
        }
        dfs(node.right, ++i, ans);
        dfs(node.left, i, ans);
    }
}

方法二：广度优先搜索

思路

我们可以对二叉树进行层次遍历，那么对于每层来说，最右边的结点一定是最后被遍历到的。二叉树的层次遍历可以用广度优先搜索实现。

算法

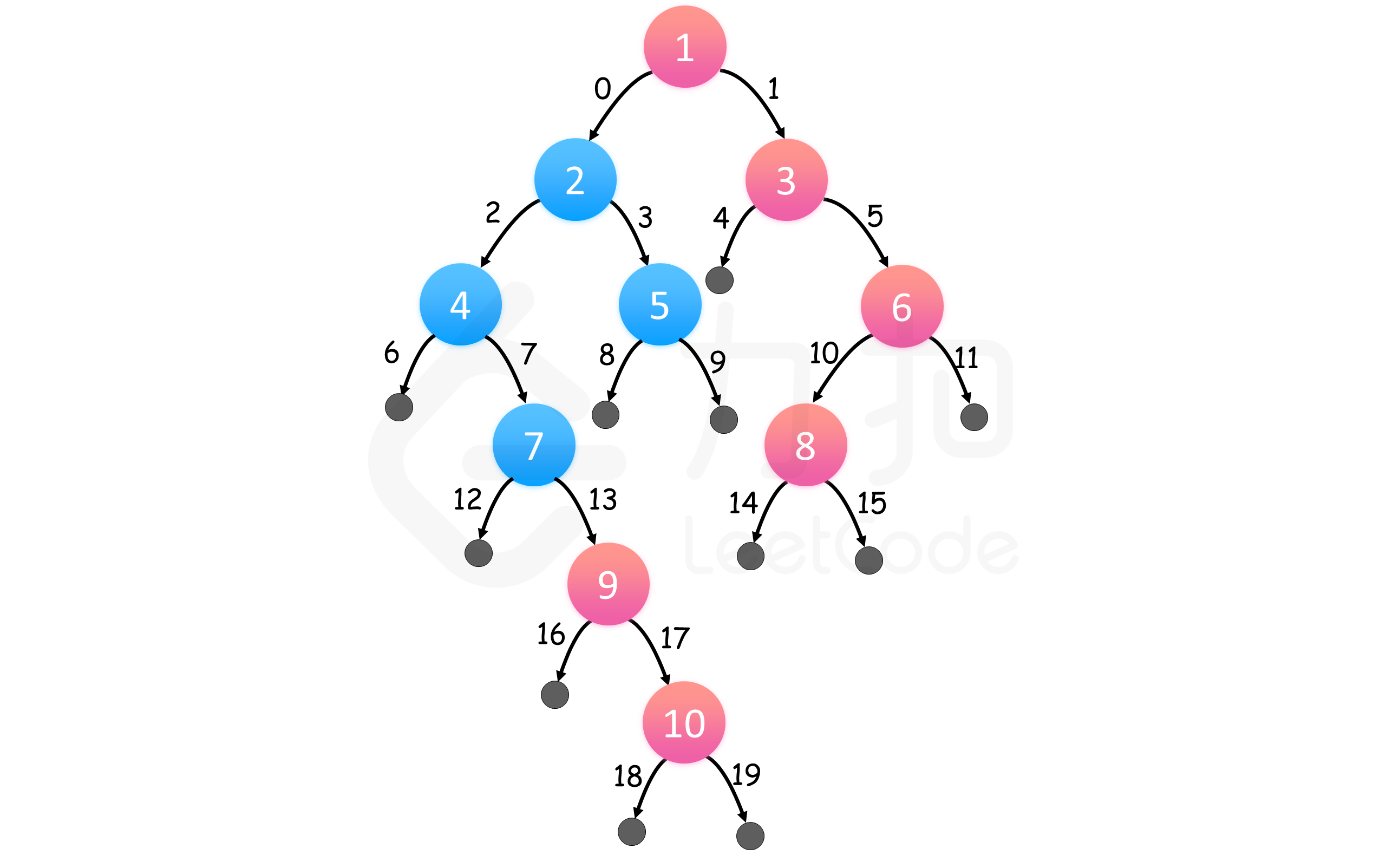
执行广度优先搜索，左结点排在右结点之前，这样，我们对每一层都从左到右访问。因此，只保留每个深度最后访问的结点，我们就可以在遍历完整棵树后得到每个深度最右的结点。除了将栈改成队列，并去除了 rightmost_value_at_depth 之前的检查外，算法没有别的改动。

上图表示了同一个示例，红色结点自上而下组成答案，边缘以访问顺序标号。

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> ans = new LinkedList<>();
        if (root == null) {
            return ans;
        }
        Deque<TreeNode> queue = new ArrayDeque<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            int temp = size;
            while (size > 0) {
                TreeNode poll = queue.poll();
                if (size == temp) {
                    ans.add(poll.val);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                size--;
            }
        }
        return ans;
    }
}